How to Model a Basic 2-body Planetary System

Here is a tutorial explaining how to model a two dimensional  2-body planetary system in Excel. It uses the Euler method of integration.

The tutorial starts with explaining the simple Newtonian laws acting on the two planets.

There are essentially just two forces acting on each body at any time: the inertia and the gravitational attraction. During each small time step, from the distance between bodies we can calculate the gravitational forces and from the Newton’s second law we can further calculate the acceleration. From acceleration and the initial speed (the speed at the beginning of the time step) we can calculate the speed at the end of each time step and from all the above known quantities we can find the position at the end of the time interval.

This iterative process is (dynamically) repeated over and over and the solution is plotted on a 2D scatter chart. A detailed step-by-step Excel-VBA implementation is further shown.

Recommending this site to your friends would be highly appreciated. Thanks for your support!

[sociallocker][/sociallocker]

Creating a basic planetary system in Excel

by George Lungu

* For the model presented here it is recommended that you use Excel 2003 or older. The 2007 will be either excessively slow.

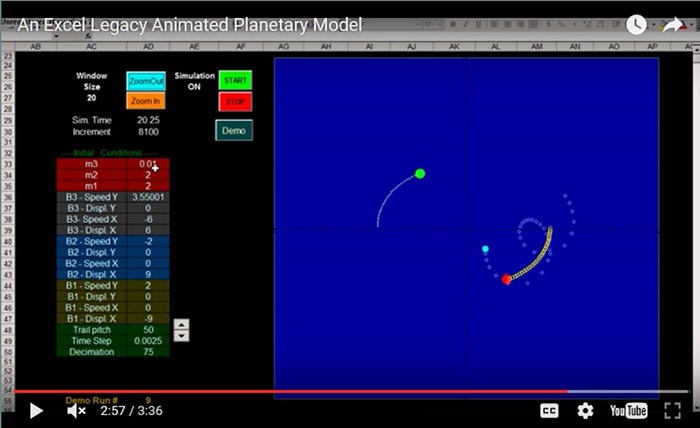
We want to create the following model:

Some basic theory from high school:

u=r/|r|
F = m*a – Newton’s 2nd law
F = u *k*m1*m2 / r^2 – Newton’s universal attraction formula

That was not a very rigorous. Pay attention to a few details:

1.- The forces acting on each body have the same direction and absolute value but opposite sense
2.- We are talking attraction not repulsion!
3.- The acceleration has the same direction and sense with the force or gravity.
4. Of course because this problem is in 2-dimenssional we need to solve it separately along x and y axes

2D vector decomposition

F2=-F1

F1x = F1*cos(a)
F1y = F1*sin(a)
x1 x2
F1 = k*m1*m2 / ((y2-y1)^2+(x2-x1)^2)
cos(a) = (x2-x1) / sqrt((y2-y1)^2+(x2-x1)^2)
sin(a) = (y2-y1) / sqrt((y2-y1)^2+(x2-x1)^2)

 

From Newton’s second law (F = m*a) and the decomposition formulas we can therefore write the x and y components of the accelerations of both bodies as:

a2=-a1

a1x = k*m2* (x2-x1) / ((y2-y1)^2+(x2-x1)^2)^(3/2)
a1y = k*m2* (y2-y1) / (( y2-y1)^2+(x2-x1)^2)^(3/2)
a2x = k*m1* (x1-x2) / ((y2-y1)^2+(x2-x1)^2 )^(3/2)
a2y = k*m1* (y1-y2) / ((y2-y1)^2+(x2-x1)^2 )^(3/2)

 

We also know the definition of acceleration as the derivative of speed with respect to time:

ax = dvx/dt or ay = dvy/dt

for a very small time increment we can assume that the acceleration is constant and re-write :

ax_current =(vx_current – vx_previous)/dt
ay_current =(vy_current – vy_previous)/dt

From here we can derive the following:

vx_current = vx_previous + ax_current *dt
vy_current = vy_previous + ay_current *dt <- Very important

Similarily:

vx = dx/dt or vy = dy/dt  – for a very small time increment we can assume that the speed is constant and re-write :

vx-current =(xcurrent – xprevious)/dt
vy-current =(ycurrent – yprevious)/dt

From here we can derive the following: xcurrent = xprevious + vx-current *dt <- Very important

ycurrent = yprevious + vy-current *dt

Outline:

a1x = k*m2* (x2-x1) / ((y2-y1)^2+(x2-x1)^2)^(3/2)
a1y = k*m2* (y2-y1) / ((y2-y1)^2+(x2-x1)^2 )^(3/2)
a1x = k*m1* (x1-x2) / ((y2-y1)^2+(x2-x1)^2 )^(3/2)
a1y = k*m1* (y1-y2) / ((y2-y1)^2+(x2-x1)^2 )^(3/2)

vx_current = vx_previous + ax_current *dt
vy_current = vy_previous + ay_current *dt

xcurrent = xprevious + vx-current *dt
ycurrent = yprevious + vy-current *dt

The above formulas are all we need to build a planetary system.

So how is the differential equation system solved?

In the previous page you can see 3 different categories of formulas:

– Acceleration/Force calculations -> yellow formulas (any time: a=F/m or F=ma)
– Speed calculation -> green formulas
– Coordinate calculations -> blue formulas

A pure spread sheet type solution:

The time in this case time will increase down the column. Each row will represent a discrete moment of time.

Advantages of the pure spreadsheet solution:

1. Requires practically no VBA (Visual Basic for Applications).
2. It is very fast

There are 2 disadvantage of the tabular solution:

1. The number of time steps is limited
2. The files are large

As we mentioned before, time advances vertically along the column.

The arrows and their colors relate to each type of equation:

Initial Conditions:

t[0] Speeds Coordinates
(Constants) ——>
time step – dt
t[1]
Forces Speeds Coordinates
t[2] Forces Speeds Coordinates
t[3] etc etc etc

 

Some important points:

The forces at time t[n] are calculated from the coordinates at time t[n-1] -> this is a compromise which gives decent solutions as long as dt is small enough (see the yellow formulas).
The speeds are calculated from the previous speeds (at t[n-1]) and the current accelerations (see the green formulas).
The coordinates are calculated from the previous coordinates and the current speeds (see the blue formulas).

 

A sequential type solution:

There is just one row of calculations. A basic VBA macro will create an infinite loop.

Advantages of the pure spreadsheet solution:

1. It can run forever (no fixed/limited number of steps). It can be stopped and restarted.
2. The Excel files are small.

The only disadvantage of the sequential solution is that it is slower than the previous (instantaneous) version.

In our case this does not matter since the simulation will be display limited ( around 20- 40 frames per second depending on the computer used and the chart size).

The macro will copy the speed and coordinate values from the active row (t[n]) to the following row.

The arrows and their colors relate to each type of equation:

t[n]

Forces Speeds Coordinates
time step – dt
t[n-1] (Constants) ——> Speeds Coordinates

The speeds and coordinates at t[n-1] are copied from the speeds and coordinates at t[n]. Therefore the formulas are using their old results to calculate the results in an infinite loop.

So, how is this whole thing implemented in Excel?

The following slides are cookbook-style.

There is no need to understand the previous sections. Just follow the recipe!

Create the input data area

Cell “A1”: Initial Conditions
Cell “A2”: x1 Cell “A3”: y1
Cell “A4”: x2 Cell “A5”: y2
Cell “A6”: v1x Cell “A7”: v1y
Cell “A8”: v2x Cell “A9”: v2y
Cell “A10”: k
Cell “A11”: dt
Cell “A13”: Zoom
Cell “A14”: m1
Cell “A15”: m2
Cell “A20”: Index
Cell “A21”: Trail Size

Input data area – figures I use font size 16 / bold

The only formula is in the cell “B20”: = L27/B11-1

For the rest of the cells just plug in those numbers as a starter.

Create spin button “k” – This button will change the gravitational constant on-the-fly.

View -> Toolbars -> Control Toolbox -> Spin Button (drag create)

In the control toolbox hit “Design Mode” then right click the button and select “Properties” Change the following:

(Name): k
Min: 0
Max: 200

 

Macro associated to button “k”:

Sub k_Change()
Range(“B10”) = k.Value
End Sub

 

Create spin button “Zoom”:

– This button will change the Zoom on-the-fly

View -> Toolbars -> Control
Toolbox -> Spin Button (drag create)
Right click the button and select “Properties”
Change the following:
(Name): Zoom
Min: 1
Max: 50

 

Macro associated to button “Zoom”:

Private Sub Zoom_Change()
Range(“B13”) = Zoom.Value ^ (1 + Zoom.Value / 100)
With ActiveSheet.ChartObjects(“Chart 1”).Chart
.Axes(xlCategory).MinimumScale = – Range(“B13”)
.Axes(xlCategory).MaximumScale = Range(“B13”)
.Axes(xlValue).MinimumScale = – Range(“B13”)
.Axes(xlValue).MaximumScale = Range(“B13”)
End With
Range(“C17”).Select
End Sub

 

Create spin button:

“Trail_Size”
This button will change the trail size on-the-fly:

View -> Toolbars -> Control
Toolbox -> Spin Button (drag
create)
Right click the button and
select “Properties”
Change the following:
(Name): Trail_Size
Min: 0
Max: 500

 

Macro associated to button “Trail_Size”:

Private Sub Trail_Size_Change()
Range(“B21”) = 10 * Trail_Size.Value
Range(Range(“D29”).Offset(Range(“B21”), 0), _
“L5000”).ClearContents
End Sub

Just a line break in VBA (the line was split in 2 by using “ _”

 

Create button “Start_Pause”:

This button will start or pause the simulation.

On Draw menu: Auto Shapes -> Basic Shapes -> Rounded.
Rectangle (drag)
On Draw menu: Text box -> Left Click in the Rectangle -> Type “Start-Pause”
Right Click the rectangle -> Assign macro -> Choose “Start-Pause” from menu.

Macro associated to button “Start_Pause”:

Public s As Boolean
————————————————–
Sub Start_Pause()
Just a line break in VBA (the
If s = False Then
line was split in 2 by using “ _”
s = True
Do
DoEvents
If s = False Then Exit Do
Range(“D28”, Range(“L28”).Offset(Range(“B21”), 0)) = _
Range(“D27”, Range(“L27”).Offset(Range(“B21”), 0)).Value
Loop
Else
s = False
Exit Sub
End If
End Sub

Observation

The original line of code didn’t give a trail:

Range(“D28:L28”)= Range(“D27:L27”).Value

Was replaced with:

Range(“D28”, Range(“L28”).Offset(Range(“B21”), 0)) = _
Range(“D27”, Range(“L27”).Offset(Range(“B21”), 0)).Value

Which creates a trail with programmable length behind each planet

 

Create button “Reset”:

This button will reset the simulation:

On Draw menu: Auto Shapes ->
Basic Shapes -> Rounded
Rectangle (drag)
On Draw menu: Text box ->
Left Click in the Rectangle ->
Type “Reset”
Right Click the rectangle ->
Assign macro -> Choose
“Reset_” from menu

 

Macro associated to button “Reset”:

Sub Reset_()
Range(“D28:L5000”).ClearContents
Range(“D28”) = Range(“B6”).Value
Range(“E28”) = Range(“B7”).Value
Range(“F28”) = Range(“B8”).Value
Range(“G28”) = Range(“B9”).Value
Range(“H28”) = Range(“B2”).Value
Range(“I28”) = Range(“B3”).Value
Range(“J28”) = Range(“B4”).Value
Range(“K28”) = Range(“B5”).Value
s = False
End Sub

 

The calculation area:

Cell “B26”: a1x Cell “C26”: a1y
Cell “A27”: t[n]
Cell “D26”: v1x Cell “E26”: v1y
Cell “A28”: t[n-1]
Cell “F26”: v2x Cell “G26”: v2y
Cell “B25”: accelerations
Cell “H26”: x1 Cell “I26”: y1
Cell “E25”: speeds
Cell “J26”: x2 Cell “K26”: y2
Cell “I25”: coordinates
Cell “L26”: time
Just names up to this point !

 

The calculation area – Active Formulas:

Cell “B27”: =B10*B15*B14*(J28-H28)/((J28-H28)^2+(K28-I28)^2)^(3/2)
Cell “C27”: =B10*B15*B14*(K28-I28)/((J28-H28)^2+(K28-I28)^2)^(3/2)
Cell “D27”: =D28+B27*B11/B14
Cell “E27”: =E28+C27*B11/B14
Cell “F27”: =F28-B27*B11/B15
Cell “G27”: =G28-C27*B11/B15

 

The calculation area – Active Formulas (continuation):

Cell “H27”: =H28+D27*B11
Cell “I27”: =I28+E27*B11
Cell “J27”: =J28+F27*B11
Cell “K27”: =K28+G27*B11
Cell “L27”: =L28+B11

 

Create the chart:

Click on an empty cell -> Insert -> Chart -> XY Scatter -> Finish

Create the chart – continuation

Delete Legend and Title.

Initial conditions
45
40
35
30
25
20
Initial conditions
15
10
5
0
-5 0 2 4 6 8 10 12
-10

Create the chart – continuation

– Click on any grid lines and delete them then change the charting area color to your taste.
– Change the font on both axes to 1 (using Format Axis).
– Click the white area -> SourceData Series.
25
20
15

– Remove whatever series is there and Add the following four series (type them in) ->

-5 0 2 4 6 8 10 12

Generate chart data series

Generate chart data series

 

Create the chart – continuation

In order to have the Zoom macro work right you have to name the chart “Chart 1”
You do this by selecting the chart and running the following macro:

Sub rename()
With ActiveChart
.Parent.Name = “Chart 1”
End With
End Sub

 

Finish:

Click the button “Reset” and then “Zoom”.

This will reset the calculations and resize the chart to the proper zoom level.

Click the button “Trail_Size” up and down once.

Then click the button “Start-Pause”.

Wait few seconds and click “Start-Pause” again.

Now go on the chart and adjust the colors and sizes of the bodies and their trails to your liking.

 

Tips:

You can experiment with various combinations of masses and initial conditions.

If dt is too large de simulation won’t converge.

You can change the zoom, trail size and even k during the simulation.

Be careful with k, change it slowly during the run. If you loose the bodies Reset the system and start it with the new k.

If you get stuck ask for help. In this case or if you just want do avoid the pain of creating one I can send you a copy of the original file.

 

by George Lungu <excelunusual.com>