This is a brief tutorial showing how to calculate the determinant of a matrix and the inverse of a matrix using two special spreadsheet functions MDETERM() and MINVERSE().
![]()
MDETERM() & MINVERSE() – two important Excel spreadsheet functions for matrix manipulations
by George Lungu
– Using Excel built-in matrix operation functions might improve calculation
efficiency but it definitely makes model development and verification easier by
decreasing the complexity and number of formulas.
-This tutorial will briefly introduce the reader to two different spreadsheet
formulas for matrix manipulations:
=> MDETERM() – used to calculate the determinant of a matrix
=> MINVERSE() – used to calculate the inverse of a square matrix
– These functions are very useful for solving systems of linear equations in Excel
<excelunusual.com> by George Lungu
The MDETERM() function:
– Returns the determinant of a square matrix. You can read more about determinants on Wikipedia website. The
determinants are used to calculate solutions of linear systems of equations using Cramer’s rule. MDETERM is
calculated with an accuracy of approximately 16 digits, which may lead to a small numeric error when the calculation
is not complete. For example, the determinant of a singular matrix may differ from zero by 1E-16.
Syntax: MDETERM(array)
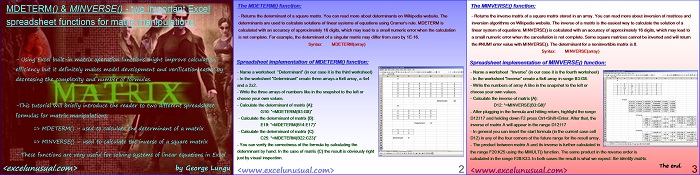
Spreadsheet implementation of MDETERM() function:
– Name a worksheet “Determinant” (in our case it is the third worksheet)
– In the worksheet “Determinant” create three arrays a 6×6 array, a 4×4
and a 2×2.
– Write the three arrays of numbers like in the snapshot to the left or
choose your own values.
– Calculate the determinant of matrix {A}:
G10: “=MDETERM(B3:G8)”
– Calculate the determinant of matrix {B}:
E19: “=MDETERM(B14:E17)”
– Calculate the determinant of matrix {C}:
C25: “=MDETERM(B22:C23)”
– You can verify the correctness of the formula by calculating the
determinant by hand. In the case of matrix {C} the result is obviously right
just by visual inspection.
<excelunusual.com> 2
The MINVERSE() function:
– Returns the inverse matrix of a square matrix stored in an array. You can read more about inversion of matrices and
inversion algorithms on Wikipedia website. The inverse of a matrix is the easiest way to calculate the solution of a
linear system of equations. MINVERSE() is calculated with an accuracy of approximately 16 digits, which may lead to
a small numeric error when the cancellation is not complete. Some square matrices cannot be inverted and will return
the #NUM! error value with MINVERSE(). The determinant for a noninvertible matrix is 0.
Syntax: MINVERSE(array)
Spreadsheet implementation of MINVERSE() function:
– Name a worksheet “Inverse” (in our case it is the fourth worksheet)
– In the worksheet “Inverse” create a 6×6 array in range B3:G8.
– Write the numbers of array A like in the snapshot to the left or
choose your own values.
– Calculate the inverse of matrix {A}:
D12: “=MINVERSE(B3:G8)”
– After plugging in the formula and hitting return, highlight the range
D12:I17 and holding down F2 press Ctrl+Shift+Enter. After that, the
inverse of matrix A will appear in the range D12:I17
– In general you can insert the start formula (in the current case cell
D12) in any of the four corners of the future range for the result array.
– The product between matrix A and its inverse is further calculated in
the range F20:K25 using the MMULT() function. The same product in the reverse order is
calculated in the range F28:K33. In both cases the result is what we expect: the identity matrix.
The end.
by George Lungu <excelunusual.com>