This is an addition to a previous post, introducing the reader to different ways of calculating the moment of a force and the torque of a couple. This information will be useful in aircraft dynamics models.
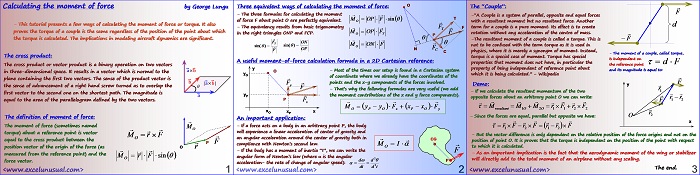
Calculating the moment of force
by George Lungu
– This tutorial presents a few ways of calculating the moment of force or torque. It also
proves the torque of a couple is the same regardless of the position of the point about which
the torque is calculated. The implications in modeling aircraft dynamics are significant.
The cross product:
The cross product or vector product is a binary operation on two vectors
in three-dimensional space. It results in a vector which is normal to the
plane containing the first two vectors.
The sense of the product vector is the sense of advancement of a right hand screw turned as to overlap the
first vector to the second one on the shortest path.
The magnitude is equal to the area of the parallelogram defined by the two vectors.
The definition of moment of force:
The moment of force (sometimes named torque) about a reference point is vector equal to the cross product between the position vector of the origin of the force (measured from the reference point) and the force vector.
<excelunusual.com>
Three equivalent ways of calculating the moment of force:
– The three formulas for calculating the moment of force F about point O are perfectly equivalent. O
– The equivalency results from basic trigonometry in the right triangles
A useful moment-of-force calculation formula in a 2D Cartesian reference:
– Most of the times our setup is found in a Cartesian system
of coordinate where we already have the coordinates of the points and the x-y components of the forces involved.
– That’s why the following formulas are very useful (we add the moment contributions of the x and y force components).
An important application:
– If a force acts on a body in an arbitrary point P, the body
will experience a linear acceleration of center of gravity and
an angular acceleration around the center of gravity both in
compliance with Newton’s second law.
– If the body has a moment of inertia “I”, we can write the F
angular form of Newton’s law (where a is the angular
acceleration- the rate of change of angular speed):
<excelunusual.com>
The “Couple”:
-“A Couple is a system of parallel, opposite and equal forces
with a resultant moment but no resultant force.
Another term for a couple is a pure moment. Its effect is to create
rotation without any acceleration of the center of mass.
-The resultant moment of a couple is called a torque. This is
not to be confused with the term torque as it is used in
physics, where it is merely a synonym of moment. Instead,
– The moment of a couple, called torque,
torque is a special case of moment. Torque has special
is independent on properties that moment does not have, in particular the the reference point
property of being independent of reference point about
and its magnitude is equal to:
which it is being calculated.” – Wikipedia
Demo:
– If we calculate the resultant momentum of the two 1
opposite forces about an arbitrary point O we can write:
– Since the forces are equal, parallel but opposite we have:
– But the vector difference is only dependent on the relative position of the force origins and not on the
position of point O. It is proves that the torque is independent on the position of the point with respect
to which it is calculated.
– As an important implication is the fact that the aerodynamic moment of the wing or stabilizer
will directly add to the total moment of an airplane without any scaling.
The end.
<excelunusual.com>