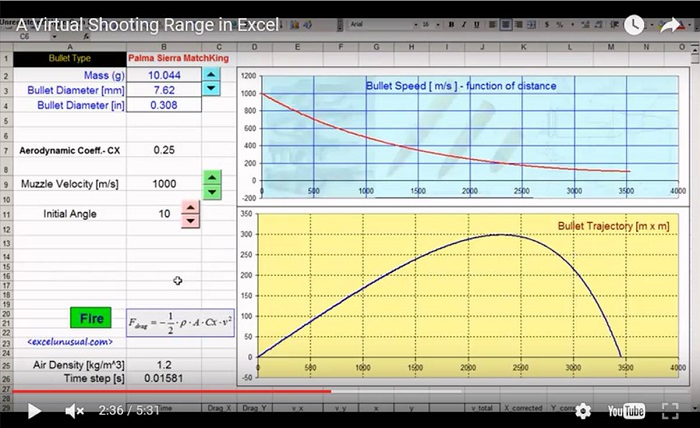
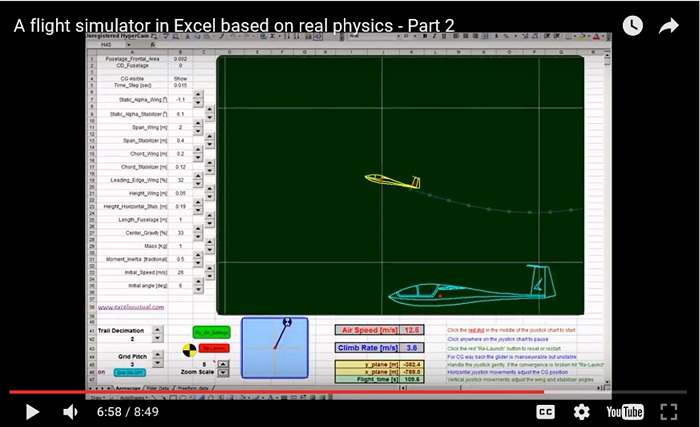
In the previous section, the main wing airfoil and the horizontal stabilizer airfoil were simulated using Xflr5.
The three coefficients, lift, drag and moment were then interpolated on charts in Excel using 4th and 5th order polynomials.
This section shows a few tricks about how to easily introduce those 60 equations as spreadsheet formulas in Excel ranges.
It also presents a simple linear interpolation method across the Reynolds number range.
We need to do this since we simulated both airfoils withing a Reynolds range of 20,000 to 200,000 with a discrete increment of 20,000.
Longitudinal Aircraft Dynamics #2- 2D polar interpolation
by George Lungu
– This section finishes the extraction of the cl, cd and cm coefficients for the horizontal
stabilizer airfoil then it uses the polar data for both the main wing and the stabilizer to create a
2D interpolation across a series of then Reynolds numbers and a range of angles of attack.
CM-stabilizer
The resulting polynomials for the horizontal stabilizer:
y = 6E-08×5 + 6E-10×4 – 3E-05×3 + 5E-07×2 + 0.0024×1 – 9E-06
y = 6E-08×5 + 4E-10×4 – 3E-05×3 + 8E-07×2 + 0.0025×1 – 1E-05
y = 5E-08×5 + 2E-07×4 – 3E-05×3 + 5E-05×2 + 0.0025×1 – 0.0009
y = -5E-09×5 – 5E-09×4 – 1E-05×3 + 2E-06×2 + 0.0021×1 – 5E-05
y = -9E-08×5 + 9E-07×4 – 2E-06×3 – 0.0001×2 + 0.0022×1 + 0.0013
y = 2E-09×5 – 6E-07×4 – 1E-05×3 + 0.0001×2 + 0.0016×1 – 6E-05
y = -1E-08×5 – 1E-09×4 – 1E-05×3 + 2E-06×2 + 0.0026×1 – 4E-05
y = -3E-08×5 – 7E-07×4 – 2E-05×3 + 5E-05×2 + 0.0032×1 + 1E-05
y = -6E-09×5 – 1E-08×4 – 2E-05×3 + 6E-06×2 + 0.0028×1 – 0.0003
y = -6E-08×5 + 1E-06×4 – 1E-05×3 – 0.0003×2 + 0.0021×1 + 0.0029
y = 5E-10×5 – 2E-06×4 – 1E-07×3 + 0.0012×2 + 3E-06×1 + 0.0217
– The extraction of these polynomial equations took me only about 15 minutes. This means that in the future models one can get a full set of data for an airfoil with three different wing configurations (two flap positions) in about one hour – not that bad.
– Attention! I added a “1” after the next to last term of each equation (after “x”). The equation is still valid but this will save us a lot of effort soon. CD-stabilizer
CL-stabilizer
y = 6E-10×5 – 2E-06×4 – 2E-07×3 + 0.0013×2 + 4E-06×1 + 0.0162
y = 2E-06×5 + 2E-06×4 – 0.0008×3 – 0.0002×2 + 0.1195×1 + 0.0036
y = 2E-08×5 – 3E-06×4 – 8E-06×3 + 0.0013×2 + 0.0003×1 + 0.0134
y = 2E-06×5 + 2E-06×4 – 0.0009×3 – 0.0003×2 + 0.1219×1 + 0.0039
y = 2E-11×5 – 2E-06×4 + 7E-08×3 + 0.0013×2 – 2E-05×1 + 0.012
y = 2E-06×5 + 9E-07×4 – 0.0008×3 – 0.0002×2 + 0.1191×1 + 0.0056
y = -3E-08×5 – 2E-06×4 + 3E-06×3 + 0.0012×2 + 0.0001×1 + 0.011
y = 2E-06×5 – 5E-07×4 – 0.0008×3 + 8E-05×2 + 0.1157×1 + 0.0018
y = 3E-09×5 – 2E-06×4 + 1E-06×3 + 0.0012×2 – 0.0004×1 + 0.0097
y = 2E-06×5 – 1E-06×4 – 0.0008×3 + 0.0002×2 + 0.1165×1 + 0.001
y = 4E-09×5 – 2E-06×4 – 1E-06×3 + 0.0012×2 + 0.0001×1 + 0.0094
y = 2E-06×5 + 8E-08×4 – 0.0008×3 – 5E-05×2 + 0.1154×1 + 0.0049
y = 1E-08×5 – 2E-06×4 + 2E-06×3 + 0.0012×2 – 0.0001×1 + 0.0085
y = 2E-06×5 – 3E-08×4 – 0.0008×3 + 7E-06×2 + 0.1148×1 – 0.0006
y = -4E-09×5 – 2E-06×4 + 1E-06×3 + 0.0011×2 – 9E-05×1 + 0.009
y = 2E-06×5 + 1E-06×4 – 0.0008×3 – 8E-05×2 + 0.1168×1 + 0.0012
y = -7E-08×5 – 1E-06×4 + 2E-05×3 + 0.0011×2 – 0.0008×1 + 0.0077
y = 2E-06×5 – 7E-08×4 – 0.0009×3 + 8E-06×2 + 0.1187×1 + 0.0007
y = 2E-06×5 – 2E-06×4 – 0.0009×3 + 0.0004×2 + 0.1203×1 – 0.0049
The flying wing Atlantica in the background – www.wingco.com
Transferring the equations in Excel:
– We will describe a procedure of using the VBA editor to transfer the 60
equations as formulas in a worksheet with very little effort.
– Rename the second worksheet in the workbook “Longitudinal_Stability_Model”
– Name cell B1 “Alpha_wing”, cell B2 “Alpha_stabilizer” and cell B3 “Re”
(range A1:A3 will contain labels).
– Copy the first group of ten equations (cl for the main wing), then open the VBA editor and paste them
within a sub called “copy-paste()”.
– Highlight the equations (red text) => Find=>
Replace => in the “Find What” box type “x”
and in the “Replace With” type “*Alpha_wing^”
=> Replace All
-Keeping all the red text highlighted replace
all “y” with [N5], then manually change the
number to the right of each N so that it starts
with a 51 and it ends with 60
-After all this is done enclose the right side
of the equations in quotation marks. Also
make sure to add an equal sign between
the first quotation mark and the beginning
of the equation for each equation.
-What you got is shown to the right:
– Now run the macro once by placing the cursor somewhere within the text of the macro and hitting the “Run” triangular button on top. This macro will fill range N51:N60 with the formulas for cl(Alpha_wing) for ten different Reynolds numbers.
<excelunusual.com
2
Transferring the equations in Excel – continuation:
– There are a total of 60 formulas bundled in six groups
– Use the same procedure to introduce the rest of 50 in
the spreadsheet (of course you need to step one column to
the right while introducing a new group). Now instead
of “Alpha_wing” you need to use “Alpha_stabilizer”.
– The final result is shown in the snapshot at the right.
– In the left column (M51:M60) I introduced the Reynolds numbers corresponding to each polynomial.
The interpolation:
– Using the polynomial formulas, the spreadsheet will calculate all the 6o values of the parameters for the
current angle. Now we just need a basic linear interpolating scheme.
– A linear interpolation scheme will mean than if the cur-
rent Reynolds number is situated somewhere between two current
of the ten preset Reynolds numbers, interpolation formula
will calculate a linear weighted average of the function
values for the immediate Reynolds number neighbors.
– Check out the CL_wing interpolation illustration to the right.
– From triangle similarity we have:
<excelunusual.com>
3
The final interpolation formula:
– Since we don’t have simulation results for Reynolds numbers below 20,000 or above 200,000 we will
limit the coefficients to the values calculated for those extreme numbers (see the implementation below,
namely the formulas for T51 and T61 are different than the rest).
Worksheet implementation of the interpolation formula:
– T51: “=IF(Re<$M51,N51,0)”
– T52: “=IF(AND(Re<$M52,
Re>=$M51),N51+(N52-N51)*(Re-$M51)/($M52-
$M51),0) then copy T52 down to T60
– T61: “=IF(Re>$M60,N60,0)” then copy T51:T61
up to Y51:Y61
– Range T51:Y61 contains segments of the
interpolation formula
– T65: “=SUM(T51:T61)” then copy T65 up to Y65
– Range T65:Y65 contains the final interpolation
results for the 6 coefficients.
– Range T49:Y50 and range T63:Y64 contain
labels
To be continued…
<excelunusual.com>
4