Flight Simulator Tutorial #1 – the joystick and a ground mesh

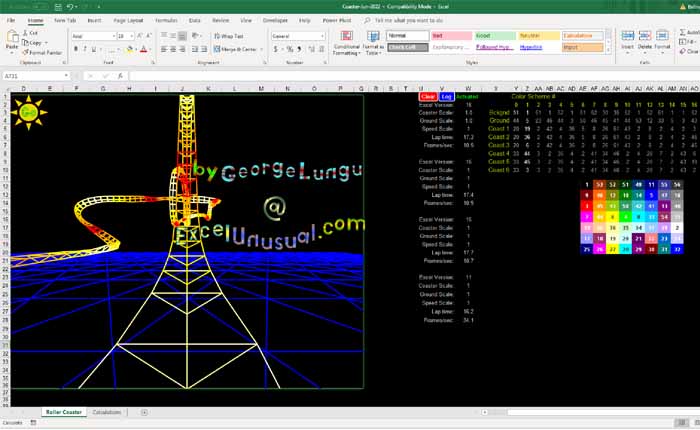
This is the first section of a tutorial explaining how to build a 3D flight simulator in Excel. This part deals with creating a joystick and a triangular ground mesh.

The joystick model was explained in a previous post from January 2011 and the ground mesh was already used in the 3D roller-coaster.

[sociallocker][/sociallocker]

A Basic Flight Simulator in Excel #1 – using a virtual joystick to control the pitch and roll angles of a wireframe object in the 3D space

by George Lungu

– We start here a series of tutorials about the implementation
of a basic Flight simulator in Excel 2003. The landscape for
this simulator will be a basic ground plane built in the form of
a triangular mesh, together with some other objects to be
determined later.

– Using the mouse driven virtual joystick developed before in
this blog we can control the pitch and roll angles of the
airplane, hence being able to perform 3D maneuvers.

– No aerodynamics effects are included in this basic model.

– The first part of the tutorial handles the joystick and the
ground mesh.

<excelunusual.com> by George Lungu

The virtual joystick:

– We will use elements of a previously created virtual
joystick model.

– Open a new worksheet and name it “Flight_Simulator”.

– Rename the first worksheet “Tutorial_1”.

– The joystick will be implemented as a 2D scatter chart.

– Clicking the chart will start the “JoyStick” macro which
continuously updates (in range B50:C50) the relative mouse coordinates relative to the initial click point on the

– Cells A50, A52 and A53 contain labels.

– Range B50:C50 contain the relative x-y coordinates of screen (when the macro was triggered).

Public Declare Function GetCursorPos _

Lib “user32” (Some_String As POINTAPI) As Long

Type POINTAPI

X As Long
Y As Long
the mouse relative to the initial click point. End Type

– Range B52:C52 contains the previously mentioned x-y
Dim RunPause As Boolean coordinates (from range B50:C50) but limited to +/- 100.
—————————————————————————
– Range B53:C53 is the origin of the joystick on the chart Sub JoyStick()
Dim Pt0 As POINTAPI
and this range is filled with two zeros.
Dim Pt1 As POINTAPI

– The 2D scatter chart has both axes scaled to [-100, 100] and the data plotted is from the range B52:C53.

RunPause = Not RunPause
GetCursorPos Pt0
Do While RunPause = True
– The “JoyStick()” macro seen to the right, was previously explained and a few more details are given in the next page. For additional insight, the reader is advised to read the Joystick tutorial from January 2011.

DoEvents

GetCursorPos Pt1
[B50] = Pt1.X – Pt0.X
[C50] = -Pt1.Y + Pt0.Y
Loop
End Sub

<excelunusual.com> 2

A few explanations about the “JoyStick()” macro:

The following are declarations:
Declaration of a special API (Application
Public Declare Function GetCursorPos _
Programming Interface) function which
Lib “user32” (Some_String As POINTAPI) As Long
retrieves the cursor position
Type POINTAPI
Declaration of a special structure (Point API) used as the output type of the previous
X As Long
API function. It is essentially the pair of coordinates (as long integers) of the cursor
Y As Long
on the screen started to be measured from the upper left corner of the screen.
End Type
Boolean variable declaration which has the role of a “switch”, keeping

Dim RunPause As Boolean
track if the macro is running or is stopped. This will allow the macro to
be started or stopped using the same button
Declaration of the macro
Sub JoyStick()
Dim Pt0 As POINTAPI Declaration two Point API type structures, one as initial click coor-
Dim Pt1 As POINTAPI dinates and the second as the current (dynamic) cursor coordinates
RunPause = Not RunPause Boolean “flip”, if the macro is stopped this will start it and vice versa
Assigns variable “Pt0” the initial click coordinates
GetCursorPos Pt0
Conditional “Do” loop declaration (start)
Do While RunPause = True
Always add this statement if you ever need to stop the loop
DoEvents
manually or update a chart while the loop is running
GetCursorPos Pt1
Every loop cycle assigns “Pt1” the cursor coordinates
[B50] = Pt1.X – Pt0.X
Every loop cycle calculate the relative coordinates and display them in the
[C50] = -Pt1.Y + Pt0.Y
range “B50:C50” (figure out why I wrote those formulas the way I wrote them)
Loop End of “Do” loop
End Sub    –   End of macro declaration

<excelunusual.com> 3

The ground plane:

– We will use here the type of ground plane used before in
the roller coaster model. To the right you can see a 3D
snapshot of that ground plane.

– We will generate the ground as a triangle mesh having
40×40 triangles.

– In order to get that type of mesh, we need to create 40 x 40
triangles and place them staggered just like in the picture to
below (which shows a small 3×3 grid demo created using
nine triangles).

Generating the vertices:

– In order to illustrate the principle we will use a
small 3×3 grid.
– For this 3×3 mesh of triangles we have a 4×4
array of vertices (in red). In general for an n x n
array of triangles we need an (n+1) x (n+1) array of
vertices

– Using the notation L for the side of the equilateral triangle we can write the following relationship:
L/2

<excelunusual.com> 4

The x, y and z vertex matrices:

– We will chart the ground plane as a single curve on a 2D scatter chart. B

– Since there are 40 x 40 = 1600 triangles and each triangle is charted as a
four point group (A=>B=>C=>A) on the chart, a (4 x 1600) = 6400 point
curve will be charted to represent the ground plane.

– We need to be able to make invisible any triangle which has at least one
vertex behind the observer, otherwise annoying artifacts will be noticed in the image (I observed this effect by chance in previous models).

– To be able to withdraw triangles from the visible area of the chart we need to create a table with 6400 x-y
data points and 1599 additional blank rows, one blank row between each 4 data rows corresponding to each
triangle. This way if a certain triangle falls behind the observer we can replace its vertices with very large
numbers (9999 for instance) and the triangle will disappear from view.

– Due to the blank row in the data table between each triangle and its neighbors, each triangle will be disjoint
(unconnected) from its neighbors. This way, by moving a triangle out of view will not leave “strings” attached
to it’s visible neighbors. Again I observed this “attached strings” effect in previous models and the only way I
was able to get rid of it was by inserting blank rows in the data table.

– We will define a 123 x 41 x-y-z Vertex array having the x-y-z data for 41 x 41 vertices:

– We will also define a “Landscape” array whose elements will be added to the z-coordinates in the “Ground” array.
first vertex
– We could have just used a single 3-column table for the x-y-z vertex data but having a 2-dimensional individual table makes it more easy to insert non-flat data (hills and mountains for
instance) and chart this data easier. The picture to the rigt shows how the data is packed in the first two rows of this table.
y41 y42 y43 y44 y80 y81
z41 z42 z43 z44 z80 z81
<excelunusual.com> 5

Creating the vertex matrices for the ground plane:

– Create a general ground plane
parameter area:

– The ranges U73:U74, U76:U78
U80, U130 and U180 are labels.
– V73:V74 contain the geometrical parameters of the triangles:
V73: “=100”
V74: “=sqrt(3)*V73/2
h
-Fill V76:V78 with zeroes for now. We can plug formulas in the
offset area later if we ever need to do so.

Create a “Landscape” array: For now fill all the range V211:BJ251 with zeroes. This could later be filled
with various landscape effects (valleys and hills).

Create the “x-y-z
Vertex” array: V81: “=V$76”, W81: “=V81+$V$73”
V82: “=V$77 then copy this one cell to the right (cell W82)
V83: “=$V$78+V211” then copy this one cell to the right (cell W83)

Copy range V81:W83 to V84:W86 and change the following V84: “=V$76+$V$73/2”
Change V85: “=V82+$V$74” and copy this cell to the right (to cell W85)
Copy range V84:W86 to V87:W89 and change V87: “=V$76”
Copy range V84:W89 to range V90:W203
Copy range W81:W203 to range BJ81:BJ203 and you finished the vertex array.
to be continued…

by George Lungu <excelunusual.com> 6